All Images
Research News
Klein Bottle is a Real Natural in the Zoo of Geometric Shapes
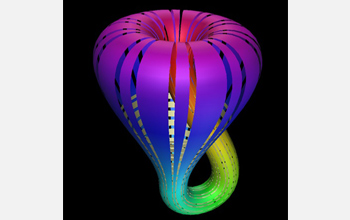
A two-dimensional representation of a Klein bottle--a shape with no inside or outside, just one continuous surface. A true Klein bottle needs at least four dimensions; in other words, it can't be blown from glass. Two- and three-dimensional representations like this one exist to help us visualize the topology, but they are not completely faithful to the original shape. The surface cannot be built in two- or three-dimensional space without self-intersection, as shown here with the "handle" passing through the side of the surface.
Credit: Thomas Banchoff, Brown University, and Davide Cervone, Union College.
Download the high-resolution JPG version of the image. (47 KB)
Use your mouse to right-click (Mac users may need to Ctrl-click) the link above and choose the option that will save the file or target to your computer.

Stanford mathematician Gunnar Carlsson.
Credit: Stanford University
Download the high-resolution JPG version of the image. (49 KB)
Use your mouse to right-click (Mac users may need to Ctrl-click) the link above and choose the option that will save the file or target to your computer.
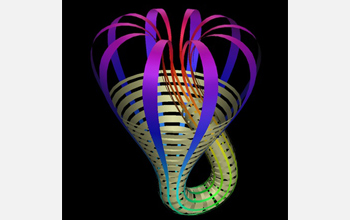
A two-dimensional representation of the Klein bottle shape with wide bands removed to make it easier to see the interior connection. Two of the colored bands are Mobius strips, but the others are orientable strips with a full twist, each looping through the handle and over the top twice.
Credit: Thomas Banchoff, Brown University, and Davide Cervone, Union College.
Download the high-resolution JPG version of the image. (60 KB)
Use your mouse to right-click (Mac users may need to Ctrl-click) the link above and choose the option that will save the file or target to your computer.


