Multimedia Gallery
Donuts, math, and super-dense teleportation
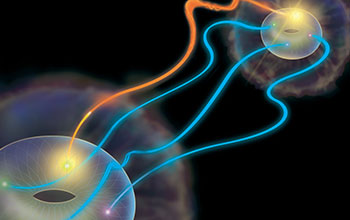
Quantum teleportation is a method of communicating information from one location to another without moving the physical matter to which the information is attached. In this demonstration of super-dense teleportation of quantum information, "Alice" (near) selects a particular set of states to send to "Bob" (far) using the hyper-entangled pair of photons they share. The possible states Alice may send are represented as the points on a donut shape, here artistically depicted in sharp relief from the cloudy silhouette of general quantum state that surrounds them. To transmit a state, Alice makes a measurement on her half of the entangled state, which has four possible outcomes shown by red, green, blue and yellow points. She then communicates the outcome of her measurement (in this case, yellow, represented by the orange streak connecting the two donuts) to Bob using a classical information channel. Bob then can make a corrective rotation on his state to recover the state that Alice sent.
More about this image
Since it was first theorized in 1993, quantum teleportation has been achieved by a number of research teams around the world. However, current experimental methods require extensive resources and/or only work successfully a fraction of the time. Now, by taking advantage of the mathematical properties intrinsic to the shape of a donut--or torus, in mathematical terminology--a research team led by physicist Paul Kwiat of the University of Illinois at Urbana-Champaign has made great strides.
Using the new protocol, the researchers have experimentally achieved 88 percent transmission fidelity, twice the classical upper limit of 44 percent. The protocol uses pairs of photons that are "hyper-entangled"--simultaneously entangled in more than one state variable, in this case in polarization and in orbital angular momentum--with a restricted number of possible states in each variable. In this way, each photon can carry more information than in earlier quantum teleportation experiments. At the same time, this method makes Alice’s measurements and Bob’s transformations far more efficient than their corresponding operations in quantum teleportation: the number of possible operations being sent to Bob as the key has been reduced, hence the term "super-dense."
This work was supported in part by the National Science Foundation (grants PHY 0903865, PHY 13-14748, PHY 13-33903 and DMS 12-01886).
To learn more about this research, see the NSF News From the Field story Donuts, math and superdense teleportation of quantum information. (Date image taken: 2012-2014; date originally posted to NSF Multimedia Gallery: July 25, 2017)
Credit: Image by Precision Graphics; copyright Paul Kwiat, University of Illinois at Urbana-Champaign
See other images like this on your iPhone or iPad download NSF Science Zone on the Apple App Store.
Images and other media in the National Science Foundation Multimedia Gallery are available for use in print and electronic material by NSF employees, members of the media, university staff, teachers and the general public. All media in the gallery are intended for personal, educational and nonprofit/non-commercial use only.
Images credited to the National Science Foundation, a federal agency, are in the public domain. The images were created by employees of the United States Government as part of their official duties or prepared by contractors as "works for hire" for NSF. You may freely use NSF-credited images and, at your discretion, credit NSF with a "Courtesy: National Science Foundation" notation.
Additional information about general usage can be found in Conditions.
Also Available:
Download the high-resolution JPG version of the image. (1.6 MB)
Use your mouse to right-click (Mac users may need to Ctrl-click) the link above and choose the option that will save the file or target to your computer.