Multimedia Gallery
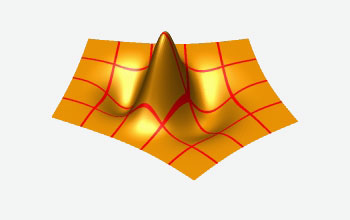
Bicubic Subdivision-Surface Wavelets (Image 2)
Subdivision surfaces. Subdivision surfaces are limit surfaces that result from continual refinement of meshes. Wavelets are mathematical functions that allow us to coarsen meshes and retain the detail between the original mesh and the coarser version. We have developed a new wavelet scheme that complements a known subdivision method called "Catmull-Clark" subdivision. This illustration shows our method when used with a very complex surface. The general idea is to use the wavelet scheme to reduce the number of elements describing the surface, then use the complementary subdivision method to reconstruct the surface in the best way. (This research was supported in part by the National Science Foundation.) [Image 2 in a series of 4. See Image 3.] (Year of image: 2002)
SORRY: THIS IMAGE IS NOT AVAILABLE IN HIGH-RESOLUTION FORMAT
Credit: Courtesy of Martin Bertram
Images and other media in the National Science Foundation Multimedia Gallery are available for use in print and electronic material by NSF employees, members of the media, university staff, teachers and the general public. All media in the gallery are intended for personal, educational and nonprofit/non-commercial use only.
Images credited to the National Science Foundation, a federal agency, are in the public domain. The images were created by employees of the United States Government as part of their official duties or prepared by contractors as "works for hire" for NSF. You may freely use NSF-credited images and, at your discretion, credit NSF with a "Courtesy: National Science Foundation" notation.
Additional information about general usage can be found in Conditions.
Also Available:
Download the high-resolution JPG version of the image. (28 KB)
Use your mouse to right-click (Mac users may need to Ctrl-click) the link above and choose the option that will save the file or target to your computer.