
| NSF Workshop | · | October 28-29, 1999 | · | Arlington, Virginia |
 |
National Science Foundation |
| C. H. Bennett | IBM |
| D. P. DiVincenzo | IBM |
| N. Gershenfeld | MIT |
| H. M. Gibbs | University of Arizona |
| H. J. Kimble | Caltech |
| J. Preskill | Caltech |
| U. V. Vazirani | UC/Berkeley |
| D. J. Wineland | NIST |
| C. Yao | Princeton University |
Any opinions, findings, conclusions, or recommendations expressed in this report
are those of the participants, and do not necessarily represent the official views,
opinions, or policy of the National Science Foundation.
Quantum Information Science (QIS) is an emerging field with the potential to cause
revolutionary advances in fields of science and engineering involving computation,
communication, precision measurement, and fundamental quantum science. The roots of this
field go back about twenty years, when pioneers such as Charles Bennett, Paul Benioff,
Richard Feynman, and others began thinking about the implications of combining quantum
mechanics with the classical Turing computing machine.
The field of QIS began an explosive growth in the early to mid 1990’s as a consequence
of several simultaneous stimuli: Peter Shor demonstrated that a quantum computer could
factor very large numbers super-efficiently. The semiconductor industry realized that the
improvement of computers according to Moore’s law would all too soon reach the quantum limit,
requiring radical changes in technology. Developments in the physical sciences produced trapped
atomic ions, advanced optical cavities, quantum dots, and many other advances that made it possible
to contemplate the construction of workable quantum logic devices. Furthermore, the need for secure
communications drove the investigations of quantum communication schemes that would be tamper proof.
In the course of supporting leading-edge research, several divisions at NSF had been
supporting QIS-related projects for some time. However, the growing excitement and opportunities
in QIS called for a careful examination of the NSF’s role in this new field, particularly since
QIS required fundamental research in many areas of science and technology to reach its potential.
Furthermore, QIS represents an important scientific basis for other national programs involving
the quantum world, such as the Nanoscience and Technology Program. Strong investments in QIS by
defense agencies and by science agencies around the world also indicated the perceived importance
of QIS.
In this context, Robert Eisenstein, Ruzena Bajcsy, and Eugene Wong, Assistant Directors
for the NSF Directorates of Mathematical and Physical Sciences, Computer and Information
Science and Engineering, and Engineering, respectively, formed the QIS Working Group to
organize a workshop to further explore NSF’s role in this field. The Working Group then
recruited the QIS Steering Committee, consisting of leaders of the QIS community. The Steering
Committee then organized the QIS workshop, which took place in Arlington Virginia, October 28-29,
1999. It was attended by approximately 100 scientists and engineers from all related disciplines.
The workshop itself was an extremely stimulating event, due in part to the presence of a large
fraction of the international leaders in the field. As one person put it: you could raise almost
any question in QIS, and the pioneer on that point would be there to address it.
The workshop comprised oral sessions, breakout sessions, and an evening town meeting,
which included further contributions and much discussion. The agenda and a list of attendees
are appended. After the meeting the Steering Committee, listed on the first page of the workshop
report, assembled an overview of the field, and made several recommendations regarding the role
of NSF in meeting the needs of the field. Logistics for the workshop itself were handled very
capably by Denise Henry. The report was reformatted for NSF systems by Ramona Winkelbauer,
while publishing services were provided by Kelly DuBose and the NSF Publishing and Information
Dissemination Service. The report is now being distributed widely throughout the QIS community
and among federal agencies. The QIS Working Group is optimistic that the NSF will be responsive
to the recommendations of this report.
Note that the report does not contain references to the literature. This was a deliberate
decision to make the report as generally accessible as possible, without the normal scholarly
detail and bibliographic information. There are a number of web sites that contain both
historical and current research information on the field of QIS. Those listed below will link
with others:
http://www.QUBIT.ORG/
http://www.euroquantum.org/
http://theory.caltech.edu/~preskill/ph229/
Finally, we would like to express our deep gratitude to the Steering Committee for
their service in organizing and writing the report on the NSF QIS workshop. The meeting was
an exceptionally stimulating experience for those in attendance, and the report is as wise as
it is compelling. We believe that this will be a significant event in the field of QIS.
NSF Quantum Information Science Working Group:
Joseph L. Dehmer, Physics Division, MPS
Michael J. Foster, Division of Experimental and Integrative Activities, CISE
Lawrence S. Goldberg, Division of Electrical and Communications Systems, ENG
John W. Lightbody, Jr., Physics Division, MPS
Arthur Sanderson, Division of Electrical and Communications Systems, ENG
Hollis H. Wickman, Division of Materials Research, MPS
Quantum information science (QIS) is a new field of science and technology, combining and
drawing on the disciplines of physical science, mathematics, computer science, and engineering.
Its aim is to understand how certain fundamental laws of physics discovered earlier in this
century can be harnessed to dramatically improve the acquisition, transmission, and processing of
information. The exciting scientific opportunities offered by QIS are attracting the interest
of a growing community of scientists and technologists, and are promoting unprecedented interactions
across traditional disciplinary boundaries. Advances in QIS will become increasingly critical to our
national competitiveness in information technology during the coming century.
The information technology revolution of the past several decades has been driven by steady
advances in the miniaturization of electronic circuitry on silicon chips, allowing performance to
double roughly every 18 months ("Moore’s law"). But in fewer than 20 years, this shrinkage
will reach atomic dimensions, necessitating a new paradigm if progress is to continue at anything
like the rate we have become used to. Accordingly, considerable thought and long-range planning are
already being devoted to the challenges of designing and fabricating devices at the atomic scale and
getting them to work reliably, a field broadly known as nanotechnology.
However, it has long been known that atoms and other tiny objects obey laws of quantum physics
that in many respects defy common sense. For example, observing an atom disturbs its motion,
while not observing it causes it to spread out and behave as if it were in several different
places at the same time. Until about five years ago, such quantum effects have mostly been seen
as a nuisance, causing small devices to be less reliable and more error-prone than their larger
cousins.
What is new, and what makes QIS a single coherent field despite spanning several traditional
disciplines, is the realization that quantum effects are not just a nuisance, but in fact can be
exploited to perform important and otherwise impossible information-processing tasks. Already
quantum effects have been used to create unbreakable codes, and a quantum computer, if one can
be built in the future, could easily perform some computations that would take longer than the
age of the universe on today’s supercomputers. The way in which quantum effects speed up computation
is not a simple quantitative improvement, like solving a hard problem more quickly by using a faster
processor or many processors working in parallel. Rather it is a qualitative improvement, like the
improvement one gets from calculating with decimal instead of Roman numerals. For the first time,
the physical form of information has a qualitative rather than merely a quantitative bearing on how
efficiently the information can be processed, and the things that can be done with it.
For this reason, even aside from its technological implications, QIS is an intellectually exciting
field, with far-reaching implications for the basic mathematical and physical sciences, both
theoretical and experimental. It is already providing a wholly new language for describing how
Nature works, and new ways of thinking about a wide variety of scientific and technical questions.
As with any revolutionary scientific insight, the long-term implications cannot be clearly anticipated,
but we are confident that they will be profound. We also expect that the emergence of QIS will have an
extensive eventual impact on how science is taught at the college and secondary level, and will bring a
deeper understanding of quantum physics to a broad segment of the lay public.
While the potential economic impact of QIS is enormous, so are the problems that must be overcome
before new quantum technologies can come to fruition. These problems are broad and deep, encompassing
theory, experiment, and engineering. It is important to build the foundations of QIS that will provide
the tools to solve these problems and enable progress toward more specific technical goals.
The development of QIS faces special problems because of its long time horizon and its intrinsically
interdisciplinary nature. Researchers in the field work at the margins of the traditional disciplines,
and therefore sometimes find it difficult to attain funding or to advance their careers. The very
best students are attracted by the excitement generated by QIS, but are uncertain how to pursue that
interest within a conventional academic department. Most worrisome, the excellent young scientists who
receive advanced degrees doing QIS research are often forced to leave the field because of a lack of
stable funding to support their work, despite the manifest relevance of QIS to the long-term economic
health of the nation.
The National Science Foundation can and should play the leading role in addressing these problems
and in fostering the continued success of quantum information science. We therefore recommend that:
Quantum physics, information theory, and computer science are among the crowning intellectual
achievements of the past century. Now, as the twenty-first century dawns, a new synthesis of these
themes is underway. The emerging discipline of quantum information science (QIS) is providing
profound new insights into fundamental problems relating to both computation and physical science.
The flourishing of this new field in the next century may guide the way to revolutionary advances
in technology and in our understanding of the physical universe.
The basic mathematical principles of quantum theory, which govern all known physical systems
found in Nature, were established nearly 75 years ago. It was recognized early on that these
principles imply that information encoded in quantum systems has weird and counterintuitive
properties, yet the systematic study of quantum information began surprisingly recently. The
explosive recent development of quantum information science can be attributed to two essential
converging factors. First, the deepening understanding of classical information, coding,
cryptography, and computational complexity acquired in the preceding decades has laid foundations
that are ripe for extension to the quantum realm. Second, the development of sophisticated new
laboratory techniques has provided the essential tools for manipulating and monitoring the
behavior of single quanta in atomic, electronic, and nuclear systems.
While today’s digital computers process classical information encoded in bits, a
quantum computer processes information encoded in quantum bits, or qubits. A qubit is a
quantum system that can exist in a coherent superposition of two distinguishable states, and
can be entangled with other such systems. The two distinguishable states might be, for
example, internal electronic states of an individual atom, polarization states of a single
photon, or spin states of an atomic nucleus. Entanglement is a subtle quantum kind of correlation
having no classical equivalent, and can be roughly described by saying that two systems are
entangled when their joint state is more definite and less random than the state of either
system by itself. Two obvious properties of classical information are that it can be read and
copied without being disturbed, and that the state of a composite system can be fully specified
by specifying the state of each of its parts. But information carried by a quantum system flouts
such common-sense principles. Indeed, quantum information can be exploited to perform tasks that
would be impossible or very difficult in a classical world.
For example:
Of the recent theoretical discoveries concerning quantum information, one of the most important
and unexpected is that noisy quantum devices (if not too noisy) can reliably store and
process suitably encoded quantum states. Ordinarily, complex quantum states like those that arise
during intermediate stages of a quantum computation are extraordinarily fragile. But if a logical
qubit is encoded, not as a single physical qubit, but instead in the form of entanglement among
several physical qubits, it becomes far more robust. The new quantum error-correcting codes and
fault-tolerant methods will be an essential part of any future effort to create, maintain, and
manipulate intricate many-qubit quantum states.
With ongoing technological improvements, quantum information processing of moderate complexity
should soon be feasible in a variety of physical implementations. It is reasonable to hope that
one such implementation will eventually enable a full-scale quantum computer, but not any time soon.
The technology of quantum cryptography is more mature and much closer to commercial realization.
We also anticipate that QIS research will have a substantial impact on other quantum technologies,
such as nanoscale engineering and precision metrology. Irrespective of the long-term technological
implications, new capabilities for quantum information processing will undoubtedly drive exciting
new discoveries in basic science.
It can also be foreseen that the emergence of quantum information science will have an extensive
impact on science education. Quantum mechanics is usually taught at the undergraduate and graduate
levels as part of the standard physics and chemistry curriculum, but the emphasis is more on
applications than on developing a solid comprehension of the subject’s strange and seductive
foundations. A course in quantum information science, by contrast, creates the opportunity and
motivation for the student to confront the bare foundations without distractions. Students of
physics, chemistry, mathematics, computer science, and engineering have the necessary background
to benefit from such a course at an early undergraduate level. With appropriate modifications, it
could even be given in high school, providing a valuable introduction to one of the great scientific
ideas of the twentieth century, and a compelling illustration of the dictum that the universe is
stranger and simpler than we can imagine.
The potential of quantum information technology is starting to be recognized by commercial
companies and the defense establishment. But for this potential to be properly fulfilled, stable
long-term support aimed at foundational scientific issues will be sorely needed. In recognition
of this need and the importance of the field, a major initiative in quantum information has been
launched in Europe. In the US, the National Science Foundation can nurture the development of
quantum information science far more effectively than more mission-oriented agencies, or profit-seeking
companies.
Future advances in quantum information science will require the combined effort of people with
expertise in a wide variety of disciplines, including mathematics, computer science and information
theory, theoretical and experimental physics, chemistry, materials science, and engineering. This
profoundly interdisciplinary character is one of the most exhilarating aspects of the field. NSF
can accelerate progress by encouraging collaboration and interaction among workers with widely
disparate training and expertise. Furthermore, progress in quantum information can be sustained only
by a substantial inflow of new talent, so it is also especially important to promote interdisciplinary
education that will enable students to contribute effectively to this emerging scientific enterprise.
Quantum information science has arisen in response to a variety of converging scientific
challenges. One goal is to probe the foundations of the theory of computation. What limits are
imposed on computation by the fundamental laws of physics, and how can computational power be
enhanced by exploiting the structure of these laws? Another goal is to extend the theory of
communication. What are the ultimate physical limits on the performance of a communication channel,
and how might quantum phenomena be harnessed by new communication protocols? Yet another challenge
is to understand and overcome the quantum effects that constrain how accurately we can monitor and
manipulate physical systems. What new strategies can be devised to push back the frontier of
quantum-limited measurements, or to control the behavior of intricate quantum systems?
While quantum information science is a broad and rapidly expanding field, there are a few
underlying recurrent themes. The theory of classical information, computation, and communication
developed extensively during the twentieth century. Though undeniably useful, this theory cannot
fully characterize how information can be used and processed in the physical world — a quantum world.
Some achievements of quantum information science can be described as generalizations or extensions
of the classical theory that apply when information is represented as a quantum state rather than in
terms of classical bits (Fig. 1).
What makes this quest intellectually compelling is that the results are so surprising. At first
glance, quantum effects seem to compromise our efforts to store, transmit, and process information,
because quantum states are highly unstable and cannot be observed without being disturbed. Indeed,
as the components of integrated circuits continue to shrink toward the atomic scale, quantum phenomena
will pose increasingly serious limitations on the performance of information processing hardware, and
one important task of quantum information science will be to illuminate whether and how such obstacles
can be overcome. But the great surprise is that the news about quantum effects is not all bad — far
from it! The fragility of quantum information becomes a very positive feature when it is recognized
that eavesdropping on a quantum communication channel necessarily leaves a detectable imprint, so
that communicating with qubits provides better privacy than communicating with classical bits. Far
more astonishing, the intrinsic complexity of quantum information ensures that quantum systems of
modest size are endowed with truly vast computational power, so that a quantum computer acting on
just hundreds of qubits is capable in principle of performing tasks that could never be performed
by conventional digital computers.
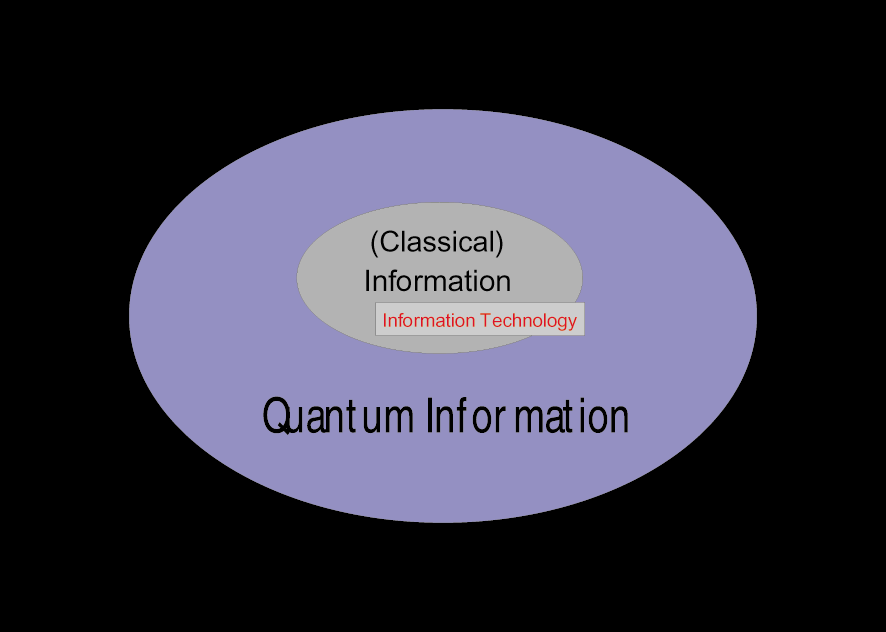
Figure 1: The well-established theory of classical information and computation is actually a
subset of a much larger topic, the emerging theory of quantum information and computation.
Another recurrent theme is quantum entanglement, the non-classical correlations exhibited
among the parts of a composite quantum system. A book expressed in classical bits can be read one
page at a time. But if a typical "quantum book" were read one page at a time, hardly any
of the information encoded in the book could be discerned. Instead, nearly all of the information
resides in the correlations among the pages. This feature of quantum information, that it is
typically encoded in the intricate correlations among the parts of a system, is the crucial way that
quantum information differs from classical information, and underlies much of the magic of quantum
computation and communication.
For example, while the number of bits of information encoded in a classical processor grows
linearly with the size of the processor, the number of parameters needed to describe the state of a
quantum processor grows exponentially with its size. The speedup achieved by quantum algorithms
can be attributed to this separation in complexity between classical and quantum information, which
arises because of the entanglement among the parts of a quantum system. Entanglement is also an
essential feature of quantum error-correcting codes. These codes protect information by storing
it in the correlations among the parts of the system; thus tearing a page from a suitably encoded
quantum book does not destroy any encoded information, since that page by itself carries no information.
Entanglement can also be viewed as a key resource that enables quantum communication protocols such
as quantum teleportation, superdense coding, and quantum key distribution. A major goal of quantum
information science is to characterize and quantify quantum entanglement, and to formulate new ways
in which it can be exploited and manipulated.
A third recurrent theme is the laboratory manipulation of matter at the level of individual
atoms or single quanta. Until recently, measurements of quantum systems were typically carried
out on ensembles of many similarly prepared systems. Now, techniques for trapping and cooling
atomic particles, and for nanofabrication of tiny electrical circuitry, are making it possible to
monitor continuously the coherent interactions of an atom, photon, or electron. The information-theoretic
approach to quantum dynamics provides an indispensable tool for understanding and controlling the
behavior of these systems.
Let us briefly review some of the milestones already reached by quantum information science. Most
have been achieved in just the past few years, and have generated a host of fascinating new questions.
Classical information theory was launched by Claude Shannon, who discovered how to quantify the
compressibility of a classical message, and how to characterize the capacity of a classical
communication channel. The compressibility of a quantum message can also be quantified, and at
least in the case where each letter of the message is a pure quantum state, the answer is closely
analogous to that found by Shannon.
A quantum channel is one that conveys qubits rather than classical bits. The capacity of such a
channel turns out to be a subtle concept, and a variety of important questions remain open. Several
different types of channel capacity can be formulated and studied; in particular, it is important
to distinguish between the amount of classical information and the amount of quantum information
that can be reliably transmitted over a quantum channel. It has been shown that the classical
capacity of a quantum channel can be enhanced if the communicating parties share a pre-existing
entangled quantum state ("superdense coding"), and that the quantum capacity can be
enhanced by two-way classical communication between the parties. One peculiar implication of the
latter result is indicated in Fig. 2.
One of Shannon’s great insights was that a random code can reach the maximum achievable
communication rate over a classical channel. A major surprise is that the corresponding statement
does not apply for quantum channels — codes with a higher asymptotic rate than the random codes
have been constructed.

Figure 2: A surprising property of the quantum channel capacity that illustrates a
counterintuitive feature of quantum information. If a quantum channel is so noisy that it has
no capacity to send quantum information, then using the channel twice in the same direction
also sends not quantum information. But if the two transmissions are in opposite directions,
the capacity is nonvanishing.
Quantum entanglement is a subtle nonlocal correlation among the parts of a quantum system that
has no classical analog. Thus entanglement is best characterized and quantified as a feature of
the system that cannot be created through local operations that act on the different parts
separately, or by means of classical communication among the parts.
In the case of a pure quantum state of a system divided into two parts,
the entanglement can be completely characterized because it can be reversibly converted to a
standard currency. If many identical copies of a given state are available, then it is possible
with local operations and classical communication to "distill" the entanglement into a
standard form — many copies of a two-qubit Bell pair. And the Bell pairs, with local
operations and classical communication, can be transformed back into many copies of the original
state, with negligible losses. Thus the number of distillable Bell pairs provides a universal
measure of bipartite pure state entanglement.
The situation is far more subtle and interesting for the case of entangled
bipartite mixed states, or for pure-state entanglement with more than two parts. For
example, some bipartite mixed states exhibit bound entanglement -- though entanglement
is necessary to create these states, none of this entanglement can be distilled into Bell pairs.
Another significant surprise is that even bipartite states with no entanglement can exhibit a
peculiar kind of quantum nonlocality. One can construct a quantum book with two pages, such
that it is impossible to read the book one page at a time, even though the two pages are not
entangled with one another.
Since entanglement cannot be created locally, an entangled state shared by
two widely separated parties can be a valuable resource (Fig. 3).
One application of shared
entanglement is a novel quantum communication protocol called quantum teleportation.
If one party (Alice) possesses a qubit in an unknown state, she cannot observe the state without
disturbing it. But if she shares a Bell pair with another party (Bob), then Alice can convey a
perfect replica of her state to Bob by sending him just two bits of classical information. In the
process, the shared Bell pair is consumed, and Alice’s original is destroyed. An odd feature of
quantum teleportation is that the unknown state can take values in a continuum; nevertheless,
thanks to the pre-existing shared entanglement, Bob needs to receive only two classical bits to
recover the perfect replica. This protocol has been convincingly demonstrated in the laboratory.

Figure 3: Two related tasks that require quantum entanglement as a resource. In quantum
teleportation, Alice receives a qubit in an unknown state, and destroys it by performing a
Bell measurement on that qubit and a member of an entangled pair of qubits that she shares with Bob.
She sends a two-bit classical message (her measurement outcome) to Bob, who then performs a unitary
transformation on his member of the pair to reconstruct a perfect replica of the unknown state. In
superdense coding, Alice receives a two-bit classical message, transmits the message by performing
a unitary transformation on a member of an entangled pair that she shares with Bob, and then sends
that qubit to Bob. Thus one qubit suffices to carry two classical bits of information.
Today’s protocols for secure Internet commerce depend on the presumed intractability of
factoring large numbers, and would become insecure if fast factoring algorithms are discovered,
or if large-scale quantum computations become practical. Although unconditionally secure encryption
and authentication techniques do exist, they are used mainly in ultra-secure settings such as the
Moscow-Washington hotline, because they depend on a resource that is difficult to provide in a
commercial setting — a supply of truly random key information shared between the communicating
parties but kept secret from everyone else. Quantum key distribution (QKD) provides a secure way
of generating such key information.
Unlike other potential applications of quantum information science, quantum
key distribution is practical with current technology, at least over moderate ranges such as
tens of km of optical fiber, or ground-to-satellite optical links. Prototype QKD systems operating
up to 48 km over conventional optical fiber, and 1 km through open air at ground level, are
already functioning. An intermediate experimental goal for QIS research, easier than building a
full-scale quantum computer, is the construction of quantum repeaters, which would make quantum key
distribution feasible over arbitrarily large distances.
Quantum key distribution has recently been proved "unconditionally secure" against an
adversary who eavesdrops on the quantum transmission in any way allowed by the laws of quantum mechanics,
but only under idealized assumptions that do not yet correspond to existing practical implementations.
In all likelihood this gap can be closed, by a combination of theory (strengthening the existing proofs
to cover more realistic sources, in particular dim coherent states) and experiment (single-photon
sources and improved detectors). While current QKD implementations have concentrated on demonstrating
basic feasibility, future implementations will include a quantitative analysis of potential
eavesdropping and the privacy amplification protocols used to defeat it, so as to optimize the
rate of safe key generation for any given combination of source, channel, and detector.
The classical theory of computational complexity is founded on the modern Church-Turing thesis,
which asserts that any "reasonable" model of computation can be efficiently simulated
on a probabilistic Turing machine (a universal computer with access to a random number generator). But
as far as we know, simulation of an n-qubit quantum computer on a classical computer requires a
computation time that grows exponentially in n. Thus, while the theorems of classical complexity
theory will stand forever as mathematical truths, they do not accurately portray the computational power
woven into the laws of Nature.
Rather, the computational model dictated by physical law is the quantum Turing machine,
or the equivalent quantum circuit model; these models can efficiently and accurately simulate the evolution
of any quantum system governed by interactions that are local in space and time. A quantum circuit consists
of wires and gates, but where the wires carry qubits, and the gates are unitary transformations. A computer
that can execute just one generic two-qubit gate is adequate to perform universal quantum
computation -- it can approximate any unitary transformation acting on n qubits to any desired
accuracy. In the quantum circuit model, it is also assumed that qubits can be initialized in a particular
standard state and measured in a particular standard basis. The final output of a quantum computation is
obtained by measuring the qubits. Because of the randomness of the quantum measurement procedure, typical
quantum algorithms are not deterministic; there is a probability distribution of possible outputs. Such
algorithms can nonetheless be very useful, if for example the output provides the correct solution to a
hard problem with high probability, and the correctness of the solution can be easily verified.
A dramatic example of a hard problem that can be efficiently solved by a quantum computer is the
problem of finding the prime factors of a large composite integer. Though there is no proof, it is
widely believed that prime factorization is an intractable problem on a classical computer, and indeed
the presumed intractability of this problem and related problems is the basis of much of modern
cryptography. Thus, a large-scale quantum computer would be a highly valuable code-breaking tool.
So far, only a few such explicit examples are known of quantum algorithms that achieve
superpolynomial speedups compared to the corresponding classical algorithms. Meanwhile, the broader
task of erecting a new theory of computational complexity compatible with quantum mechanics is now
well underway, though still far from complete. For example, the class of problems that are efficiently
solvable on a quantum computer (denoted BQP, for "bounded error probability, quantum polynomial
time") is known to be contained in the classical complexity class P#P; in particular,
a quantum computer can be simulated on a classical computer with a memory of polynomial size.
The natural quantum analog of the NP class for classical computation is denoted BQNP
("bounded error probability, quantum nondeterministic polynomial"). A problem is in NP if a
trial answer offered by a "witness" can be verified in a time that grows no faster than a
polynomial of the size of the input to the problem. Similarly, a computational problem is in BQNP if
its solution can be verified in polynomial time on a quantum computer, but where
the "witness" is a quantum state. It has been shown that the ground state energy problem
is BQNP complete — the problem is to decide whether a "local" Hamiltonian (a sum of
Hermitian operators, each involving a constant number of qubits) has an eigenvalue smaller than a
specified energy E. Thus any problem in BQNP can be reduced to an instance of the ground
state energy problem after running for a polynomial time on a quantum computer. This result is the
quantum analog of the Cook-Levin theorem, the centerpiece of classical complexity theory.
The study of interactive proofs, which combine randomness, non-determinism and interaction,
has proved to be one of the most fruitful directions in classical computational complexity theory.
A problem is in the class IP if a "prover" with great computational power can convince
a "verifier" that he/she is able to solve the problem correctly. Recently quantum
interactive proof systems have been defined and studied: a problem is in QIP if the prover can
convince the verifier, but where now prover and verifier exchange qubits rather than classical bits.
Quite surprisingly, it has been shown that one and one half rounds of quantum communication between
prover and verifier are as powerful as many rounds of quantum communication.
Suppose that we are confronted by a very large unsorted database containing N items,
and we are to locate one particular item. This search problem is particularly important, since
it captures the essence of NP-hard problems such as satisfiability. A classical exhaustive
search requires of order N steps to succeed with appreciable probability. But surprisingly,
a quantum computer can perform the search in only of order N1/2
steps. The quantum search algorithm achieves a quadratic
speedup relative to the classical search, in contrast to the superpolynomial speedup achieved by
the quantum factoring algorithm, but quantum searching can be applied to a much broader spectrum
of interesting problems.
Apart from devising new quantum algorithms that are faster than classical
algorithms, it is also of great interest to obtain lower bounds on the resources needed
by a quantum computer to solve a problem. In fact, for the database search problem, a tight lower
bound has been found, so that the known quantum search algorithm is actually optimal — no faster
solution is possible. Although quadratic quantum speedups can be attained for a wide variety of
problems, some problems have been formulated for which it can be shown that no quantum speedup
is possible at all.
The power of quantum computation arises from the exponentially-many hidden degrees of freedom in
the state of an n-qubit system. Can these degrees of freedom be tapped for super-efficient
communication? The answer to this question is actually quite subtle. On the one hand, it is known
that at least n qubits must be transmitted to send a message that is n bits long. But
on the other hand, there are certain specialized communication tasks for which qubits really do
offer a substantial advantage.
For example, suppose that two parties each maintain a calendar with N entries,
and they want to find a time when both are available for a meeting. In the worst case, they will
need to exchange of order N bits of classical information in order to have a reasonable
probability of successfully arranging their date. The same task can be performed by exchanging only of order
N1/2 log N qubits of quantum information. Qubits offer a far
more dramatic advantage for the problem of dealing hands containing N1/2
from a deck of N cards. Classically, of order N1/2 bits
must be exchanged. But the same task can be performed, with a success probability
1-d, by exchanging only of order log N
log(1/d) qubits.
One of the most surprising recent developments in quantum information science, and one of the most
important, is the discovery that unknown quantum states, if properly encoded, can be protected from
errors (Fig. 4). Since the complex states that arise at intermediate stages of a quantum computation
are extraordinarily fragile, quantum error correction will be essential to prevent large scale quantum
computers from crashing.
The state of a quantum computer can be viewed as a vector in an abstract space
of very high dimension. On first acquaintance, it sounds strange that a vector that takes values in a
continuum (in contrast to the discrete values assumed by a classical bit string) can be protected against
damage. How will we know if the vector drifts slightly in an unexpected direction? The secret of quantum
error correction is to encode a quantum state in a cleverly selected subspace of a larger vector space.
Errors that move the vector in a direction perpendicular to the code subspace can easily be detected and
reversed, while errors parallel to the code subspace cause trouble. But if the code subspace is carefully
chosen, typical errors will have only a very small component along the code subspace, and encoded
information will be well protected.
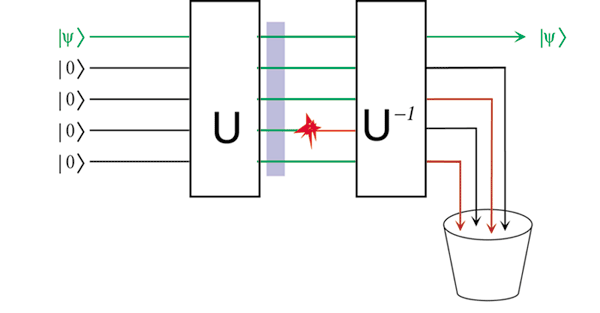
Figure 4: A simple quantum error-correcting code. A single qubit of quantum information can
be encoded as a highly entangled state of five qubits. If one of the qubits is heavily damaged by an
interaction with the environment, the encoded quantum state can still be recovered perfectly.
The principles of quantum error correction were discovered less than five years ago, and the subject
has developed explosively. Many explicit examples of quantum error-correcting codes have now been
constructed. Nearly all of these fit into a beautiful unifying framework: the code subspace can be
characterized as a simultaneous eigenspace of all the generators of an abelian group, the code’s
stabilizer group. "Good" codes have been shown to exist — the number of encoded qubits and
the number of errors that can be corrected both scale linearly with the size of the code block.
The existence of abstract quantum-error correcting codes is not in itself sufficient to ensure
that quantum information can be stored reliably. The difficulty is that recovery from error requires
a complex quantum computation, and further errors will inevitably occur as we carry out the recovery
operation. Furthermore, we want more than reliable storage, we want to be able to process quantum
information accurately. We need to devise procedures for error recovery and computation that are
sufficiently robust as to work effectively even if implemented imperfectly. In particular, errors
tend to propagate from one qubit to another when the qubits interact through the operation of a
quantum gate — our procedures must be designed to keep this error propagation under control.
In fact, such fault-tolerant procedures can be formulated for any of the stabilizer quantum
codes. When these procedures are used, quantum error correction really does improve the precision
of a quantum computation, provided that the quantum gates are sufficiently accurate, and the
decoherence times are sufficiently long. Indeed, an accuracy threshold for quantum computation
can be established: if the probability of error per quantum gate is below a critical value, then an
arbitrarily long quantum computation can be completed with negligible probability of error. The length
of the code block needed to ensure good accuracy grows only polylogarithmically with the size of the
computation to be performed.
The discovery of fault-tolerant methods has greatly improved the prospects for unleashing the power
of quantum computation in realizable devices. Moreover, the new methods ensure that very intricate
quantum systems can in principle be accurately controlled, with broad potential implications for basic
physical science and for technology.
Atomic, molecular, and optical (AMO) physics has long been at the forefront of the manipulation
and control of individual quantum systems, with particularly spectacular developments resulting from
the trapping and cooling of single electrons, ions, and neutral atoms. These advances are now
enabling realizations of conditional quantum dynamics at the single-quantum level that are suitable
for the implementation of quantum logic.
Nonlinear optics has been extended into the domain of single atoms and photons, leading to a
demonstration of a quantum phase gate in which one photon induces a conditional phase shift on
another via their mutual interactions with an atom in an optical cavity. Single trapped atoms
have been cooled to the zero point of motion, and a quantum gate has been implemented by conditionally
exciting a single phonon in an ion trap.

Figure 5: Photograph of five beryllium ions in a lithographically fabricated RF trap. The separation
between ions is approximately 10 microns.
Since these initial demonstrations, experiments with trapped ions have continued to yield
impressive achievements in the coherent manipulation of quantum systems, including the
deterministic generation of entanglement between two ions in a trap. Further experiments with
RF micro-traps will be able to extend this exquisite control of both internal states and quantized ion
motion to larger systems (Fig. 5).
Experiments with single atoms and photons in cavity quantum electrodynamics (cavity QED) have
also attained remarkable success. Number states of the radiation field have been created and quantum
non-demolition detection of single photons accomplished. By integrating the techniques of laser
cooling and trapping with those of cavity QED, real-time trapping of individual atoms has been
achieved. Atoms can be tracked with precision approaching the standard quantum limit, leading to a
new form of atomic microscopy.
On the theoretical front, AMO physics has provided important models for the implementation of
quantum information processing that bridge the gap between abstract quantum algorithms and real
physical systems. These models have stimulated new experimental advances, and have led to more
detailed understanding of the interplay between physical dynamics and quantum information. For
example, new quantum error correction protocols have been developed that are adapted to the dominant
decoherence mechanism in ion trap and cavity QED computers, including a protocol that protects against
certain types of dissipative events to all orders in the error probability.
AMO physics has led the advances in modern quantum measurement science for twenty years, in part
because the fundamental physical mechanisms associated with both coherent and dissipative processes
can be well-understood theoretically and accessed with great technical power in the laboratory. Indeed,
many experiments in AMO physics have reached and in some cases have exceeded the standard quantum limits
associated with zero-point or vacuum fluctuations.
NMR has an unusual place among the prospective approaches for manipulating quantum information. While
there are significant challenges to scaling ensemble quantum computing to large systems, it has been used
in experimental simulations of non-trivial quantum algorithms, and has led to practical applications of
quantum computing.
In NMR quantum computation, qubits are stored in the orientation of nuclear spins, which have very
long coherence times. Exchange coupling through bonds provides a coherent nonlinear interaction, and
gates are implemented by using radio frequency pulses to modify the spin evolution. Although the bonds
cannot be switched on and off, their influence can be controlled through the spectroscopic techniques of
refocusing and decoupling, so that a desired effective Hamiltonian can be synthesized from a known one. The
most distinctive feature of NMR quantum computing is that a qubit is stored, not in a single underlying
degree of freedom, but in about 1022 redundant copies.
Since the Zeeman splitting between nuclear spin states is a tiny fraction of the thermal energy in
room-temperature NMR systems, the quantum state of the spins is very highly mixed. It therefore comes
as a surprise that coherent processing of pure quantum states can be faithfully simulated in these
systems. Among the achievements attained using NMR are simulations of quantum computations that require
fewer logical steps than their classical counterparts, quantum error correction protocols, and efficient
simulations of other quantum systems. These successes have raised intriguing and fundamental questions
about the power of quantum information processing with highly mixed states.
The interaction between NMR and quantum computing has been beneficial in both directions. The
demonstration of universal computation in molecules has led the chemistry community to realize that
viewing a molecule as an information-processing device provides an entirely new language with
applications far from computation. For example, an important unsolved spectroscopic problem had been
exchanging the product operator coefficients between remote spins, so that a sensitive species could
be used to read out information from an important but less-sensitive one. This kind of exchange is
needed for the studies of complex molecular structure and function that are the foundation of modern
synthetic chemistry and drug design. Following the initial NMR experiments for quantum computing,
it was shown that the spin exchange problem could be solved by writing it in terms of the logical
SWAP operations that are a computational primitive. The experimental demonstration of this protocol
promises to have widespread applications.
Efforts are underway to make NMR quantum computing technology less expensive and more
accessible (Fig. 6).

Figure 6: A "desktop quantum computer." Inexpensive table-top devices now under development,
like the one sketched here, will be able to outperform the costly commercial NMR spectrometers
that are used in current studies of room temperature ensemble quantum computation.
Quantum information science is a very new field, so new that many promising aspects of it
have hardly been explored. Here we compile just a sampling of challenging open questions and
problems.
Many of these unsolved problems span the traditional disciplinary boundaries. A common thread
is the challenge of characterizing what can be achieved with quantum information processing, and
how it can be achieved. We emphasize in particular that the physical requirements for quantum-state
manipulation are entirely different from those for classical information processing; therefore it is
essential that investigations of the potential physical implementations of quantum information
processing be broad-based and exploratory.
While the factoring and search algorithms are exciting breakthroughs that hint at the potential
of quantum algorithms, our understanding of what quantum computers can do is still quite limited.
It is very important to seek new quantum algorithms that can speed up the solutions to interesting
problems.
The factoring algorithm makes use of a quantum Fourier transform that can be
efficiently computed for any abelian group. The same ideas enable quantum computers to break a
wide variety of cryptosystems. In fact, essentially all quantum algorithms that achieve exponential
speedups fit into a common general framework: they find a hidden subgroup in an abelian group.
Recent work shows that normal hidden subgroups in a non-abelian group can also be found efficiently.
A major challenge is to extend this framework to the general non-abelian hidden subgroup problem.
Several problems seem to be excellent candidates to be solved by efficient quantum
algorithms, but such algorithms have not yet been found. One example is graph isomorphism: given two
graphs, can one be transformed to the other by a permutation of the vertices? Graph isomorphism can
be expressed as a hidden subgroup problem in the symmetric group Sn. Other important
examples are breaking the Ajtai-Dwork cryptosystem, which involves finding short vectors in certain
types of lattices, and breaking cryptosystems based on classical linear error-correcting codes.
In the long run, one of the most important applications of quantum computers is likely to be
simulating the dynamics of quantum systems with many degrees of freedom. Much can be done to determine
how quantum computers can best be used to address simulation problems of physical interest. Examples
include the properties of quantum chromodynamics in real time or at finite nucleon density, or the
behavior of quantum antiferromagnets and strongly correlated electron systems.
A particular challenge will be to determine if M-theory is susceptible to efficient simulation on a
quantum computer. M-theory has been proposed as a unified description of all of the forces of Nature,
including gravity. It can be formulated in terms of the quantum mechanics of very large matrices, but
because of the intrinsic nonlocality of the theory, these matrices do not admit an obvious decomposition
as a tensor product of smaller systems. It would be exciting to discover that no efficient simulation is
possible, which would suggest that the computational power woven into the laws of Nature is even greater
than we now suspect.
Quantum simulation may also play an important role in the evolution of new quantum technologies.
Validating and characterizing the design of even relatively simple quantum devices will press the limits
of conventional digital computing. In particular, a quantum computer would be an extremely valuable tool
for the development of practical implementations of quantum feedback control.
The class of efficiently solvable problems on a quantum computer, BQP, is known to be contained in PSPACE,
and is unlikely to contain NP. However, we do not yet know much about its relationship to other complexity
classes. For example, is BQP contained in the polynomial hierarchy? In particular, does the power of
approximate counting suffice to simulate quantum computation? There is evidence that BQP is not contained
in MA (one-round interactive proofs), since there is an oracle relative to which the recursive Fourier
sampling problem is not contained in MA.
The recent developments on the quantum analog of NP and quantum interactive proofs open up a number
of fundamental issues. It should now be possible to classify a wide variety of problems about quantum
systems as either being efficiently simulable on a quantum computer or BQNP-complete (much like the
classification developed by the classical theory of NP-completeness). It is an open question to put
the work on quantum interactive proofs in the framework of probabilistically checkable proofs, which
is a deep and important part of computational complexity theory.
There are novel computational resources, other than time and space, that should be studied. One
interesting question arises in the context of bulk NMR quantum computation with weakly polarized
nuclear spins. Consider an n-spin system, which is described as a separable mixed state at
every step in its evolution. Thus each instantaneous state is described by a probability distribution
over orientations of n classical tops. However, if the evolution of the system is quantum
mechanical (described by quantum gates), then it is not known whether such a system can be efficiently
simulated on a classical computer, or whether it can simulate a universal quantum computation. Another
intriguing question, which can also be posed in the context of bulk NMR quantum computation, is whether
it is possible to carry out universal quantum computation if the initial state of the system is highly
mixed. One recent result addresses the power of a quantum computer in which all qubits but one are
initially in the uniformly mixed state. It was shown that if we restrict our attention to faithful
simulations of a universal quantum computation, then such mixed state quantum computers are no more
powerful than classical computers.
Apart from being important for a study of quantum computers, there are techniques of a fundamentally
quantum nature that have provided new insights into classical complexity theory. Two examples are the
linear lower bound on the communication complexity of the inner-product function and the reformulation
of the log-rank conjecture for communication complexity. It is quite possible that the new method of
quantum adversaries could provide an important new technique for classical computation as well.
Besides privacy and authentication, conventional cryptography includes other goals. For
instance, a digital signature scheme allows Alice to send a message to Bob in such a way that
Bob can verify that the message is really from Alice and that it has not been altered at all. A
zero-knowledge proof allows Alice to prove to Bob that she knows how to solve a particular problem
without Bob learning anything about how Alice’s solution works. One particularly intriguing example
is "secure distributed computation," in which two or more cooperating parties evaluate a
function of all of their inputs. Though some of the parties may be malicious or unreliable, the
computation may nevertheless be reliable (the bad parties cannot alter the result) and discreet
(the bad parties cannot learn any more about the others’ inputs than is implied by the value of
the function).
There are classical solutions to these problems, but all rely on making some sort of assumption,
such as a limitation on the computational power of a cheater. An important goal of QIS is to
formulate quantum protocols that might allow us to weaken or remove these assumptions.
Many classical cryptographic protocols are built from simpler ("primitive")
protocols. An important ‘primitive for two-party secure distributed computation’ is called bit
commitment, the mathematical equivalent of Alice’s locking a bit in a safe and sending it to Bob.
Bob cannot open the box until Alice gives him the key, but Alice cannot change her choice once
she has given the box to Bob. It has recently been shown that unconditionally secure bit commitment
is not allowed by the laws of quantum physics — if Alice and Bob have quantum computers, then
whenever Bob is unable to determine the value of Alice’s bit, Alice can safely change her bit
without Bob finding out. Still, it is of interest to develop two-party distributed computation
schemes in which cheating is computationally difficult (though not absolutely impossible) with a
quantum computer.
Since quantum computation compromises the security of much of classical cryptography, it is extremely
important to develop a new cryptography that is immune to quantum cryptanalysis. For example, are there
one-way functions that are easy for a quantum computer to evaluate, but hard for a quantum computer to
invert? To design such primitives, we need to understand the limitations of quantum computation much
better than we do today.
So far, three techniques have been developed for proving lower bounds on the running time of quantum
algorithms: the hybrid argument, the method of polynomials, and the method of quantum adversaries.
Extending this bag of tricks will better enable us to devise new cryptosystems that are invulnerable to
a quantum attack.
It has been shown that any quantum algorithm for inverting a random permutation
on N elements requires at least of order N1/2
steps. Since random permutations are
regarded as good models for one-way functions, this result provides some positive evidence for the
existence of one-way functions immune to quantum cryptanalysis. On the other hand, no non-trivial
lower bound is known for the problem of finding a collision in a random 2-1 function. Since
random 2-1 functions are regarded as good models for collision intractable hash functions
(a fundamental cryptographic primitive), it is very important to understand the complexity of
this problem.
It is of great interest to refine the estimates of the accuracy threshold for quantum computation,
as the threshold will define the specifications that must be met by the hardware components of a
future quantum computer. Current estimates vary over a broad range, depending on assumptions about
what protocol is used and how the noise is modeled; according to the most optimistic estimates,
an error probability per gate as high as 10-3 can be tolerated. It is important to
obtain more rigorous estimates that would apply to a broad spectrum of conceivable protocols.
It is also important to optimize the circuitry that implements the error recovery or the
fault-tolerant quantum gates. Perhaps an even more promising approach to improving the threshold
would be to investigate schemes for fault tolerance beyond the purview of the standard quantum
circuit model. Drawing on analogies with classical error correction techniques will very likely
be helpful.
Important computational efficiency considerations remain open. Current fault tolerant
constructions require polylogarithmic overhead in time and in space. How much can these overhead
requirements be reduced? In the classical case, constant overhead in time is sufficient, but it
is not known whether this applies in the quantum case.
Also in need of further study are more general noise models. Much work on fault tolerance has
focused on the problem of combating uncorrelated stochastic errors, but schemes that can overcome
strongly-correlated noise should also be formulated and analyzed. More generally, there is a need
to better understand how a quantum code can be devised that is well matched to the expected noise
processes in a specific physical system.
Finally, new approaches to fault tolerance should be developed that achieve robustness through
the design of the physical hardware. A particularly promising idea is to encode quantum information
in the topological properties of the entanglement of many-body systems with local interactions.
Topological quantum computation is a rich and promising subject, combining deep questions about
topology, quantum error correction, and many-body quantum dynamics.
Quantum information processing and quantum error correction will provide the laboratory scientist
with unprecedented tools; these can be exploited to devise new strategies for performing interesting
high-precision measurements.
An experimenter detects a time-dependent weak classical force by monitoring the response of a sensitive
quantum system. But since observing the quantum system necessarily disturbs it, there are intrinsic
limitations on the accuracy of the measurement. Quantum information theory has taught us that strategies
that exploit entangled quantum states can collect more information than strategies that do not, so we can
anticipate that the most precise measurement methods will require entangled probes (Fig. 7).
Much work must be done to infer what resources are required to carry out a measurement of specified accuracy, and
how best to deploy those resources under realistic laboratory conditions.

Figure 7: An example illustrating that, in a quantum setting, the best way to measure
something can be a subtle issue. Two spins point along the same axis; they are parallel in case
(a), anti-parallel in case (b). If the spins were measured one at a time,
then the information collected about the spin axis would be the same in both cases. In fact,
though, more information about the axis can be collect in case (b), because the optimal
quantum measurement is an entangled measurement that acts on both spins at once.
Closely related to the challenge of high-precision measurement is the challenge of controlling
quantum states. To control a system effectively, one needs to collect information about its behavior.
Hence quantum control is particularly delicate — monitoring a system necessarily exerts back action on
the system. Formulating effective protocols for quantum control poses daunting problems for both
theorist and experimentalist.
The entanglement of a two-part pure quantum state can be conveniently quantified by the number
of Bell pairs that can be distilled by local operations and classical communication. But it is
still not known if it is possible to express the entanglement of a pure state with more than two
parts in terms of some such standard currency. For example, it is unclear whether a
three-party "cat" state should be regarded as possessing an entirely different kind of
nonlocality than two-party Bell pairs.
A universal measure of many-particle pure-state entanglement, if one can be formulated, would
have many applications. It might enable us to identify new kinds of quantum critical points at which
the degree of entanglement of the ground state of a Hamiltonian changes discontinuously, or to
characterize which kinds of quantum dynamics are hard to simulate on a classical computer.
A deep and long-standing fundamental problem is to understand and precisely define the
transition from classical to quantum behavior. There are many systems in which quantum
effects have a strength that depends on an adjustable parameter. It is usually easy to
recognize the difference between a system that behaves very classically and one that behaves
very "quantumly," but is there a sharp boundary between the two? And if so, where
is the boundary? (Fig. 8)

Figure 8: The quantum--classical boundary. A classical computer can efficiently
simulate a system that behaves classically, but not one that behaves "quantumly."
Hence it is possible to identify a sharp transition between the quantum and classical
phases of some physical systems.
Arguably, the most interesting observation ever made about the difference
between quantum and classical is that a classical system cannot efficiently simulate a
quantum system. We can try to use this idea to establish a well defined boundary between
quantum and classical behavior. Indeed, the intrinsic accuracy threshold for quantum
computation can be regarded as just such a phase boundary. Below the critical noise rate,
there is long-range entanglement in the system, whereas above the threshold the entanglement
between two subsystems decays exponentially as the subsystems are separated. The study of
such transitions has barely begun, and there are many open questions. In particular,
universality classes and critical exponents associated with long-range entanglement are
yet to be identified.
The Standard Model of particle physics provides a marvelously
accurate description of the fundamental constituents and their interactions down to
distances of order 10-16 cm. But the most compelling fundamental questions
concern physics at the Planck scale, 10-33 cm, where spacetime undergoes strong
quantum fluctuations. While it seems hopeless to explore physics at these scales directly
in high-energy accelerator experiments, a large-scale quantum computer might provide an
incisive indirect probe of quantum gravity. At least one proposed model of physics at the
Planck scale dictates that the dynamics of the universe actually can be efficiently
simulated by a classical Turing machine. Since the factoring of numbers with of order 1000
digits is believed to be beyond the capability of any conceivable classical computer, a
quantum computer of the future that achieves such a task will convincingly rule out any such
model of Planckian physics!
Another possible way for quantum information science to illuminate the
fundamental interactions is suggested by the discovery of fault-tolerant quantum computation.
If quantum mechanics breaks down at very short distances, then we might say the "qubits" of
the fundamental theory are continually subjected to errors — that is, to deviations from unitary
evolution. Yet somehow, these errors are unseen at the larger distance scales we are currently
capable of probing. How can it be so? Until quite recently, we lacked the tools to productively
investigate this sort of question. But now hierarchical quantum error-correcting techniques have
been found that exhibit this kind of behavior: the error rate gets smaller and smaller at higher
and higher levels of the hierarchy. Could fault-tolerance be woven into the fundamental laws,
so that the error rate flows to zero in the infrared limit? A broadening interface between
quantum information science and fundamental physics can be anticipated, with tremendous
potential payoffs.
AMO physics provides powerful laboratory systems for the exploration of quantum
information processing, quantum measurement, and quantum information dynamics. Because
the relevant physical mechanisms and sources of dissipation can be understood and easily
modeled, these systems are especially well suited for testing and developing error correction
protocols. Existing experiments have achieved remarkable control of few-qubit systems. Extending
this level of control to larger systems will require understanding and eliminating various
sources of decoherence such as patch-effect fields and laser intensity and frequency fluctuations.
But given the impressive rate of progress to date, it seems reasonable to anticipate that quantum
information processing involving tens of qubits will be achieved within a decade.
Apart from their potential relevance to quantum computation and communication,
the new capabilities arising from AMO physics will push the science of precision measurement into
a radically new domain. Time-frequency standards, gravitational wave detection, and the
characterization of solid state devices at low temperature are just a few of the frontiers of
advanced metrology that will be affected.
Scaling
For quantum information processing to scale to increasing numbers of qubits, new
experimental options must be explored to avoid a debilitating increase in technical overhead.
One option in cavity QED is to move from more traditional Fabry-Perot cavities to nano-fabricated
cavities in photonic bandgap materials. It might then be possible to trap and manipulate
individual atoms by exploiting the powerful tools of lithography, while still maintaining
strong coupling between individual atoms and single photons. A different option is to build
an array of small traps, where atoms can be shuttled from one trap to another.
Quantum networks
One specific challenge is to combine the complimentary paradigms of flying and
standing qubits in the construction of quantum networks for quantum communication
and distributed quantum computation. As illustrated in Fig. 9,
multiple atom-cavity systems
located at spatially separated "nodes" could be linked via optical fibers to create
a network of quantum information processors with quantum-coherent interconnects. A complete
set of elementary network operations has been proposed and analyzed, including fault-tolerant
local processing of quantum information, transmission of quantum states between nodes, and
the distribution of quantum entanglement. If it could be realized, such a quantum Internet
might support a wide range of quantum protocols.

Figure 9: Illustration of a protocol for the realization of a quantum network. An
applied laser beam ( (t)) transfers quantum information from the
internal state of an atom in one cavity to a photon state, via the atom-cavity coupling g.
The photon travels along an optical fiber, enters a second cavity, and the information is
transferred to an atom in that cavity. Nonlocal entanglement can be created among the atoms
in the two cavities. By expanding from two cavities to a larger set interconnected by optical
fiber, complex quantum networks can be realized.
(t)) transfers quantum information from the
internal state of an atom in one cavity to a photon state, via the atom-cavity coupling g.
The photon travels along an optical fiber, enters a second cavity, and the information is
transferred to an atom in that cavity. Nonlocal entanglement can be created among the atoms
in the two cavities. By expanding from two cavities to a larger set interconnected by optical
fiber, complex quantum networks can be realized.
Optical lattices
Beyond ions traps and cavity QED, another system with promise for quantum information
processing is an "optical lattice," in which neutral atoms are trapped by the AC-Stark
shift produced by a set of intersecting laser beams. Because the atoms are neutral, they interact
very weakly with the environment. Dissipation arising from inelastic photon scattering can be
suppressed, as can other forms of dissipation such as coupling to phonons, defects, and
impurities. Optical lattices have tremendous flexibility — a wide range of properties
characterizing the lattice potential can be adjusted through laser beam geometry, polarization,
intensity, and frequency. These adjustable "knobs" permit one to design interactions
such that atoms interact strongly only during logic operations (e.g., via dipole-dipole
interactions), but otherwise are isolated from each other and the environment. Substantial
theoretical work needs to be done to assess the long-term potential of optical lattices as
quantum information processing systems.
The ideas of quantum information processing are beginning to influence the agenda of
condensed matter physics and materials science. A remarkable variety of proposed implementations
of quantum bits and gates have been put forward, and their implications for experimental
directions in these fields are being actively assessed by workers in the community.
Having been concerned for most of its history with bulk or collective properties,
condensed matter physics is now beginning to address the behavior of systems where
individual quantum properties are important. Qubits might conceivably be implemented
in any of these systems, although so far only the rudiments of quantum gate operations
have been achieved. The continuing quest for coherent information processing in a
condensed matter setting will address some of the most fundamental problems in the
quantum mechanics of individual systems.
Many specific quantum-gate technologies based on solid-state physics have been
proposed. They include:
Ultra-small superconducting structures. In these, the qubit can be embodied either
in the quantum state of flux of a SQUID (superconducting quantum interference device) or in
the quantized Cooper-pair number of a small superconducting island. Single-qubit rotation has
recently been observed (Fig. 10).

Figure 10: Quantum coherence in a superconducting Cooper-pair box. Cooper pairs of
electrons can tunnel through the Josephson junction barrier onto the island electrode, and
quantum information can be encoded in the number of Cooper pairs on the island. Coherent
oscillations in the number of pairs were recently observed.
Quantum dots. Such structures have been the focus of nano-device technology both as
optical and electronic devices. As quantum gates, their quantized electron number or spin
can function as the qubit; switching of the quantum state might be achieved either by optical
or electrical means.
Semiconductor optical microcavities. These devices, long researched for their
applications in solid-state microlasers, are approaching the point at which the coherent
manipulation of single photons is becoming a possibility. In addition, these can be coupled
to atomic-like qubits in the form of embedded single-electron quantum dots. This proposal
has many contacts with existing thrusts in optoelectronics.
Impurities in semiconductors. Integrated-circuit technology demands greater and
greater control over the precise profile of dopant impurity concentrations in semiconductor
devices. If this technology is developed to the extent that control of impurities atom-by-atom
is achieved, quantum computation might become possible. The nuclear or electronic spins of individual
phosphorus impurities are the qubits in this scheme, and transistors control operations between these
qubits.
Various other systems, which are conceivable only because of the long development of
science and technology in condensed-matter physics, have been proposed for implementing
quantum computing devices — for example, using the orbital states of electrons floating
on the surface of liquid helium, or the edge states of the quantum Hall effect. Undoubtedly,
many other proposals will emerge as the workers in the various subfields of condensed-matter
physics turn their imagination to the problem.
We envision a variety of specific ways in which quantum information science will influence
the agenda of research in condensed-matter materials science in the coming years:
Phase coherence
The observation and characterization of quantum phase coherence has been a long-standing
theme of mesoscopic physics; quantum computing gives a definite focus to this theme and asks
new questions about how systems can be tailored to exhibit a high degree of coherence. In
the superconducting community, the achievement of controlled single-qubit operations will
be tantamount to achieving the long-standing goal of Macroscopic Quantum Coherence (MQC)
in SQUIDs and related structures.
Entanglement
Some much-studied condensed matter systems, such as highly correlated electron
systems and frustrated anti-ferromagnets, have very highly entangled many-body ground
states, and the properties of the quasiparticle excitations of these systems reflect that
underlying entanglement. But quantum entanglement among quasiparticles has had
only a limited role in the description of solid-state phenomena, where single-particle
descriptions have held the dominant place. (In certain subfields, such as in the optical
physics of highly excited semiconductors, correlations among particles have received
prominent attention.) New structures being proposed will result in the controlled generation
of two-particle and eventually many-particle entanglement in a large variety of solid-state
systems; this will require theory to explore how these various forms of entanglement can be
characterized, and how well they can survive interaction with the various types of solid-state
environments.
Readout
The "readout" requirements of quantum computing will provide additional impetus
behind the drive to achieve high quantum efficiency measurements of, for example, single
spins in solids; it will require the mastery of the subtle and counterintuitive issues of
the quantum measurement problem, such as the construction of non-demolition measurements.
Solid state researchers will have to travel the road now being explored in atomic
physics, in which Schrödinger cat states are controllably created
and undone, and measurements can be performed and then reversed again.
Fabrication and control
The structures that are proposed and that will be needed for this fundamental research
will require a close encounter with state-of-the-art materials science and applied research
in fabrication and in device physics. In a few of the proposals, individual dopant
impurities in a semiconductor must be placed, one at a time, with unprecedented accuracy;
new ion-beam or scanned probe deposition techniques will have to be developed to address
this requirement. Some of the proposals for sensitive quantum measurement require the construction
of magnetic-semiconducting heterostructures that have not been previously contemplated. The
specifications of quantum gate operations put unprecedented demands on the bandwidth and precision
of high-frequency gated control of microstructures. 1/f noise phenomena must be completely understood
and suppressed in these structures. Many of these directions are ones that are already part of the
agenda of advanced device technologies, but quantum computing probably pushes some of these
technologies harder than any other computing schemes.
Communication
Quantum communications has engendered further thinking about how a solid state bit can be made
mobile, and this has brought solid-state optics into the picture. Several proposals focus on the
existence of various technologies, arising out of work on solid-state lasers, for the production
of high quality-factor microcavities; it is known that quantum dots and other small quantum
structures can be grown inside such cavities, and proposals for quantum gate operations, and
for the transmission of a qubit as a photon emitted by the cavity, have been developed and will
be the subject of future experimental research. Finally, there is even the possibility of using
electrons themselves as mobile qubits; several proposals have been made for a Bell-type experiment,
in which all steps — creation of entanglement, separation of the two particles, detection of the
quantum states — are done electronically in a mesoscopic device.
Unorthodox implementations
Solid state physics is very versatile, and while the above survey can give some idea of
how quantum information science and solid state physics may develop together in the future,
it should not preclude an unforeseen departure from this "orthodox" view. For
example, there is some discussion indicating that a recently identified gapped, fractional
quantum Hall state (the " =5/2" state)
may be the first "nonabelionic" state of matter, exhibiting quasiparticles with
non-abelian, anyonic statistics. This discovery may actually have a real bearing on quantum
information processing: calculations have indicated that nonabelionic matter may be uniquely
suited as a medium for fault tolerant quantum computation. Will
the
=5/2" state)
may be the first "nonabelionic" state of matter, exhibiting quasiparticles with
non-abelian, anyonic statistics. This discovery may actually have a real bearing on quantum
information processing: calculations have indicated that nonabelionic matter may be uniquely
suited as a medium for fault tolerant quantum computation. Will
the  =5/2 state be the basis of a quantum
computer? Probably not; but we should be open to possibilities like this, and to even
more exotic-sounding ones.
=5/2 state be the basis of a quantum
computer? Probably not; but we should be open to possibilities like this, and to even
more exotic-sounding ones.
Many groups around the world are now using NMR to investigate small quantum computers,
because of the familiarity and availability of the required spectrometers. A fundamental
limitation will come in, however, beyond roughly 10 qubits. This is because room-temperature
NMR uses a very weakly polarized sample, which leads to a partition function normalization
that decreases exponentially as qubits are added. Although experimental refinements might
reach the classical simulation limit of tens of qubits, it cannot scale beyond that. To go
further, near-unity spin polarization is needed. Although this might be achieved by cooling
the entire sample to millikelvin temperatures, that would eliminate the beneficial protection
of intra-molecular coherence through translational thermalization. A more promising alternative
is to cool just the nuclear spin system, which is routinely accomplished with optical pumping
of rare-gas atoms. An open question is whether this will be possible with more complex molecules
and in solids; if it is, the other parameters of this system are already close to what is
needed for scaling to significant sizes.
It is important to view this scaling effort in the context of the complementary experimental
approaches; as they progress they are all likely to grow together. Optical pumping for NMR draws
on insights from AMO physics, and, in turn, NMR points to techniques for manipulating ensembles
and effective Hamiltonians that are applicable to the alternatives. And the experimental progress
in NMR to date has been driving the development of higher-level quantum programming tools that
will be needed in any quantum computer.
The development of conventional information technology has been neatly separated into physical
scientists investigating underlying devices, and computer scientists working on architectures and
applications. This division in both academia and industry has resulted in many of the most
compelling questions about the meaning and manipulation of information being left neglected at
the interface between hardware and software.
In contrast, one of the most striking features of the emerging science of quantum information
is its transcendence of the division between abstract bits and physical quanta. To contribute
in an arena where information content and physical embodiment are so intimately integrated, the
early investigators needed mastery of many aspects of physics, computer science, engineering,
and mathematics. An example that illustrates the symbiosis of computer science and physics is
the successful adaptation of classical error correction ideas to quantum systems, an advance
critical to the long-term viability of the field.
QIS has stimulated strong cross links between computation science and mathematical physics,
and among areas such as AMO physics (e.g., NMR, cavity-QED, ion traps), condensed matter
physics (e.g., electron/nuclear spins in semiconductors, single-electron transistors,
coupled super-conducting systems), and engineering (e.g., nanotechnology, feedback,
scalability, quantum-limited metrology). Direct evidence of these vibrant interfaces can be
seen from the makeup of attendees at conferences and workshops on QIS.
Quantum information science is a field whose initial and future successes are clearly tied
to its interdisciplinary nature. And, as is often the case in a scientific revolution, many
researchers in QIS find themselves at the margins of their home disciplines, with their activities
stretching the conventional limits of physics, computer science, mathematics, or electrical
engineering. Indeed, a remarkable new generation of young researchers is growing up in an
intellectual environment in which the traditional distinctions of discipline make less and
less sense.
These developing cross links between diverse communities can be expected to directly
benefit not only QIS, but science and technology more broadly, by catalyzing connections
between various subfields of mathematics, physics, and engineering that might otherwise go
unexplored. A principal benefit to industry is the cadre of young scientists and engineers
who are being trained in new ways to help confront the challenges that lie beyond the end
of VLSI scaling. For example, experimental investigations of possible physical implementations
have nearly always been carried out in small laboratories, enabling students to be involved
in all aspects of the research, from nano-fabrication to control theory to quantum algorithms.
Many of the best upcoming students are attracted to the study of quantum information because
of its intellectual and technological impact. For them, QIS is not a specialized application to
be encountered late in their education, but an organizing principle that drives an enormous
appetite for learning about quantum systems and about the tools relevant for manipulating them.
This ground swell among young people manifests itself in enormously over-subscribed new courses
taught across disciplinary boundaries. Courses in QIS can be aimed at the early undergraduate
level, enabling an education in physics and other technical fields to reach a broader and more
enthusiastic audience.
The continuing investigation of the intimate connections between information and physical
systems may also enhance the role of science in society. Numerous magazines and newspaper
articles have already been published in response to the lay-person’s fascination with computers
and quantum physics. As quantum mechanics and information science continue to meld, this broad
interest in QIS will help to bring science to a growing portion of the populace.
Quantum information science has emerged as one of the most exciting scientific developments
of the past decade. As described in the preceding sections, initial advances in QIS have
encompassed a broad and remarkable landscape, ranging from super-fast quantum algorithms for
computation and communication to fault tolerant architectures for quantum computers to the
realization of quantum gates for the physical implementation of quantum logic. Beyond
contributions to fundamental knowledge, these advances in QIS are of great potential technological
significance to our society as information processing and communication march inexorably into
the quantum realm.
In attempting to understand how best to foster the continued success of QIS, one should
recognize that the most spectacular advances in the field have largely sprung from
individual "zealots" who ventured beyond the boundaries of traditional disciplines
and who did so without dedicated support for their activities (and in some cases, with active
discouragement). The QIS community is largely a self-organized group of otherwise independent
researchers drawn together by the intellectual excitement and potential of the field, sharing
a strong incentive to learn as much as possible across a broad front, since no one can say from
where the next great discovery will emerge. Moreover, the tools forged on one front are as
likely as not to be employed on another, whether in investigations of physical dynamics with
intrinsic fault tolerance, of new quantum algorithms, or of the engineering of materials for
the new quantum components.
The brief history of QIS points to the essential role of "small science" driven
by individual investigators. It is very important to continue to foster the research of
individuals, and to encourage interactions across the traditional boundaries in physics,
computer science, and engineering. Significant advances have sprung from unexpected quarters in
the past, and further surprises should be expected — not just the emergence of new research
directions but also the appearance of talented new people working in the field.
These considerations argue for stable long-term support of multidisciplinary research
carried out by investigators either individually or in small collaborations. In the current
scheme of things, there is a dearth of support for scientists and engineers whose research
is aimed at foundational issues. Moreover, there is a pressing need to overcome structural
problems of "dislocation." That is, students who are interested in quantum information
science cannot be sure in which department to pursue that interest. Having nonetheless succeeded,
these young graduates face yet another hurdle in that universities are reluctant to hire faculty
working in a new and less established area that is not well matched to the department structure in
academia.
In the end, there is no simple and obvious strategy for best fostering the continued
advancement of a new field as diverse and dynamic as QIS. For each prescription for success
there are conflicts and contradictions. For example, on the experimental front,
the "individual PI" model will become increasingly difficult to sustain since the
technical requirements for most experiments in QIS continue to become ever more daunting.
There is thus a tension between maintaining diversity in investigations of physical systems
and pursuing such investigations at the cusp of technical capability. Certainly instrumentation
programs to support technically intensive research in QIS are vital to success. But equally
certain is that the demand will greatly exceed the supply of funding for such programs. In
concert with the various government agencies, industrial research laboratories, and national
laboratories, the community will have to devise new research strategies that, on the one hand,
foster the contributions of individual PIs and, on the other hand, address the question of
optimal resource utilization.
The NSF can meet the need for stable, long-term support aimed at laying the foundations
for a new science in a way that more mission-oriented agencies cannot (and have not).
Although arguably the most spectacular results in QIS to date relate to large-scale quantum
computation for cryptanalysis, NSF programs should be much more broadly based and should
emphasize the development of a whole new area of science. As highlighted in preceding sections,
promising topics "beyond the Shor" include quantum metrology, quantum networks and
communication, and quantum components at the nanoscale. We note that, while the US (via the
NSA in particular) has taken the lead in the effort to develop a large-scale quantum computer,
we lag far behind the European community in establishing collaborations and research programs
directed toward the broader foundations of QIS.
Much work in QIS will be hard to fund through traditional mechanisms because it is
speculative and far from mainstream activities. An important role for NSF is to
encourage "far out ideas" in new areas and to sustain long-term support directed
toward "hard problems." However, the cycle of peer review and the organization of
programs tend to favor incremental progress in well established areas instead. Furthermore,
in the emerging arena of QIS, the traditional discipline-based organization of education and
research may not be appropriate. Thus meeting the needs of the QIS community poses special
problems, and we do not pretend to know the answers. Central issues are that support for QIS
research should be coordinated among the NSF divisions, and that advocacy for QIS at NSF
should be vested in some tangible form — advocates are essential to provide institutional
memory at NSF and to ensuring long-term stability.
We favor support directed toward individual investigators engaged in "small
science," which we feel will be more productive than funding concentrated in large
centers. However, we do not preclude the concept of centers altogether; the cost of
infrastructure and the benefits of collaboration could lead to a persuasive case that a
portion of funding should be directed to center support. Novel concepts may be effective,
such as "virtual centers" that promote exchanges of students and post-doctoral
scholars. NSF-sponsored workshops might also help to foster productive interdisciplinary
collaborations.
Especially important is the development of the careers of young people. Although QIS
attracts the very best students, it is difficult for these students to continue to
advance their careers after graduate school. While in part this is an unavoidable
situation in a rapidly developing new field, the NSF can play an indispensable role by
providing funding opportunities to help establish and maintain young careers. These
young people are a vital resource not only for QIS but for the nation, in view of the
ever increasing impact of information technology on our society.
Arlington Hilton, Gallery I
Day 1, October 28, 1999
Morning Session
| 8:30 – 9:00 | NSF Welcome, Introduction |
Overview talks
A. Ekert, Chair
| 9:00 – 9:35 | C. Bennett, Overview of Quantum Information |
| 9:35 – 10:10 | U. Vazirani, Quantum and Classical Complexity |
| 10:10 – 10:45 | G. Brassard, Quantum Communication and Cryptography |
| 10:45 – 11:00 | Coffee break |
| 11:00 – 11:35 | J. Preskill, Future Directions of Quantum Information Science |
| 11:35 – 12:10 | J. Kimble, Physical Implementations of Quantum Logic |
| 12:15 – 1:30 | Lunch |
Afternoon Session – Physical Systems
B. Whaley, Chair
| 1:45 – 2:15 | D. Wineland, Trapped Ion Quantum Computation |
| 2:15 – 2:45 | Y. Maguire, Ensemble Quantum Computing via NMR |
| 2:45 – 3:15 | P. Zoller, Quantum Computing with Atoms |
| 3:15 – 3:45 | R. Hughes, Activities in Quantum Information Science at LANL |
| 3:45 – 4:15 | Coffee break |
| 4:15 – 4:45 | B. Kane, Semiconductor Spin Quantum Computing |
| 4:45 – 5:15 | Y. Nakamura, Quantum Bit in a Single-Cooper-Pair Box |
| 5:15 – 5:45 | S. Koch, Quantum Effects in Excitonic Systems |
8:00 – 10:00 Town Meeting
J. Dehmer, M. Foster, L. Goldberg, Jack Lightbody, Art Sanderson, Hollis Wickman
NSF Representatives
Day 2, October 29, 1999
Morning Session
C. Caves, Chair
| 8:30 – 9:00 | A. Ekert, European Activities in Quantum Information Science |
| 9:00 – 9:30 | H. Everitt, Other U.S. Agencies Activities in Quantum Information Science |
Quantum Information and Algorithms
| 9:30 – 10:00 | D. Aharanov, Error Correction and Fault Tolerance |
| 10:00 – 10:15 | Coffee break |
| 10:15– 10:45 | A. Kitaev, Topological Quantum Computing |
| 10:45– 11:15 | D. DiVincenzo, Protecting Quantum States via Symmetrization |
| 11:15– 11:45 | S. Lloyd, Quantum Modeling |
| 11:45 – 12:15 | M. Freedman, Quantum Field Theories and Quantum Computing |
| 12:30 – 1:45 | Lunch |
| 2:00 – 4:00 | Afternoon Breakout |
Group II – Quantum Information and the Physical Sciences, Leader: J. Preskill
(with C. Hood as scribe)
Group III – Physical Implementations, Leader: J. Kimble (with N. Amer as scribe)
4:00 – 5:00 Joint session with feedback from breakout groups, including
recommendations for workshop report
5:00 Adjourn
| Name | Institution |
| Dorit Aharonov | UC/Berkeley |
| Nabil Amer | IBM/Yorktown |
| Ruzena Bajcsy | NSF |
| Charles Bennett | IBM/Yorktown |
| Joseph Bordogna | NSF |
| Jack Boudreaux | NIST |
| Giles Brassard | University of Montreal |
| Phil Bucksbaum | University of Michigan |
| Aubrey Bush | NSF |
| Denise Caldwell | NSF |
| Carlton Caves | University of New Mexico |
| Isaac Chuang | Stanford University |
| Charles Clark | NIST |
| Arnold Dahm | Case Western University |
| Frederica Darema | NSF |
| Pankaj Das | UC/SD |
| Richard de Millo | Bellcore |
| Joseph Dehmer | NSF |
| Dennis Deppe | University of Texas |
| David DiVincenzo | IBM/Yorktown |
| Mark Dykeman | Michigan State University |
| Joseph Eberly | University of Rochester |
| Robert Eisenstein | NSF |
| Artur Ekert | Oxford University |
| Stephen Elbert | NSF |
| Michael Evangelist | NSF |
| Henry Everitt | ARO |
| Amr Fahmy | Harvard Medical School |
| Yeshaiahu Fainman | UC/SD |
| Eugene Fan | DOD |
| Nancy Forbes | Litton TASC |
| Lance Fortnow | NEC Research Institute |
| Michael Foster | NSF |
| Michael Freedman | Microsoft Corporation |
| Don Gammon | Naval Research Laboratory |
| George Gamato | |
| Neil Gershenfeld | MIT |
| Hyatt Gibbs | University of Arizona |
| Gerald Gilbert | Mitre Corporation |
| Lawrence Goldberg | NSF |
| Jozef Gruska | Informatics |
| Sanjay Gupta | Virginia Tech |
| Timothy Havel | Harvard Medical School |
| Mark Heiligman | NSA |
| Peter Hendrickson | NRO |
| Richard Hilderbrandt | NSF |
| Murray Holland | University of Colorado |
| William Holton | North Carolina State University |
| Cristina Hood | Caltech |
| Richard Hughes | Los Alamos National Laboratory |
| Richard Isaacson | NSF |
| Poul Jessen | University of Arizona |
| Nick Jones | |
| Paul Julienne | NIST |
| Subhash Kak | Louisiana State University |
| Bruce Kane | University of Maryland |
| Boris Kayser | NSF |
| Galina Khitrova | University of Arizona |
| Jeff Kimble | Caltech |
| Christopher King | Northeastern University |
| Alexey Kitaev | Caltech |
| Tom Kitchens | DOE |
| Stefan Koch | University of Marburg |
| Marvin Kruger | NSA |
| Rudolph Krutar | North Carolina State University |
| Chun-Lim Lau | Booz-Allen & Hamilton Inc. |
| Jean-Pierre Leburton | University of Illinois/UC |
| Zachary Lemnios | |
| Paul Lett | NIST |
| Jack Lightbody | NSF |
| Seth Lloyd | MIT |
| Samuel Lomonaco | University of Maryland/BC |
| Yael Maguire | MIT |
| Stephen Mahoney | NSF |
| Pierpaolo Malinverni | European Commission |
| Edgar Martinez | DARPA |
| Keith Miller | DOD |
| Martin Morf | Stanford University |
| Yasunobu Nakamura | NEC Research Laboratories |
| Nasser Peyghambarian | University of Arizona |
| John Preskill | Caltech |
| Winston Roberts | NSF |
| Steven Rolston | NIST |
| Mary Beth Ruskai | University of Massachusetts/Lowell |
| John Salasin | DARPA |
| Arthur Sanderson | NSF |
| Barry Schneider | NSF |
| Keith Schwab | NSA/Caltech |
| Alexander Sergienko | Boston University |
| Francisco Serpa | |
| Louis Sica | Naval Research Laboratory |
| Karen Sollins | NSF |
| Duncan Steel | University of Michigan |
| Bruce Taggart | NSF |
| T.J. Tarn | Washington University |
| Yosef Gavriel Tirat-Gefen | |
| Nikzad Toomarian | |
| Umesh Vazirani | UC/Berkeley |
| Dan Ventura | Penn State University |
| Nolan Wallach | UC/SD |
| Ian Walmsley | University of Rochester |
| Richard Webb | University of Maryland |
| Tom Weber | NSF |
| Birgitta Whaley | UC/Berkeley |
| Hollis Wickman | NSF |
| Carl Williams | NIST |
| David Wineland | NIST |
| Andrew Yao | Princeton University |
| Zeke Zalcstein | NSF |
| Roger Ziemer | NSF |
| Peter Zoller | University of Innsbruck |