News Release 10-029
Fighting Crime With Math
Sophisticated math models give insights on crime hotspots
February 20, 2010
View a video showing how math modeling is used to understand crime spikes.
This material is available primarily for archival purposes. Telephone numbers or other contact information may be out of date; please see current contact information at media contacts.
What causes a crime wave and what measures should law enforcement use to reduce the spread of criminal offense? Researchers at UCLA and the University of California, Irvine, who are funded by the Human and Social Dynamics program at the National Science Foundation, say they may have an answer.
Andrea Bertozzi, director of applied mathematics at UCLA, says crime hotspots form either when small spikes in crime grow and spread--but not far enough to bind distant crimes together--or when a large spike in crime pulls offenders to a specific location. She says measurable reductions in crime require different policing strategies for each hotspot type.
Bertozzi's conclusions come from research involving a system of mathematical equations that uses empirical evidence for how repeat offenders move and mix in society, as well as how they choose their targets. She and her colleagues report their findings this week in the Proceedings of the National Academy of Sciences.
"To try to predict crime and devise better crime prevention strategies, you need a mechanistic explanation for how and why crime occurs," said Bertozzi. "We think we have made a big step in providing at least one core aspect of that explanation."
The research team's mathematical models are based on empirical observations of crime patterns occurring in the city of Los Angeles during the last 10 years, and may help to predict crime and devise better prevention strategies. The models factor in the locations of possible targets, such as homes, automobiles and people, as well as general environmental cues about the feasibility of committing a successful crime in a particular location. In addition, the researchers included specific knowledge offenders might have about target or victim vulnerability in the area.
Analysis of the models shows supercritical crime hotspots can form from the rapid chain reaction of lawlessness, while subcritical hotspots result from large spikes in crime that override otherwise stable crime patterns.
The mathematical models also predict how the outcomes of certain, discrete policing actions will differ between the two hotspot types. "Policing actions directed at one type will have a very different effect than policing actions directed at the second type," said Bertozzi.
The research shows that subcritical hotspots may be destroyed through certain types of police intervention, whereas supercritical hotspots will typically just move to new locations. Understanding this difference may enable law enforcement to tailor their responses to hotspots of differing types, thereby reducing or eliminating crime in an area, even after their suppression measures have been removed.
The models "provide a useful framework in which to investigate the formation of crime patterns and the impact of alternative policing strategies on crime hotspot stability," the researchers write in their report.
They write that motivated offenders search their environment for suitable targets or victims following simple behavioral routines. If an offender encounters a target in the absence of an effective security measure, then he is free to exploit that target. But, the researchers note, the immediate presence of security such as law enforcement is sufficient to deter that crime.
"Our model was originally built around a model for residential burglaries; however, based on real data we believe the ideas in the analysis likely apply to a variety of crime types," said lead author of the study Martin Short, an adjunct assistant professor of mathematics at UCLA.
"The analysis of the model says something subtle that you would not necessarily be able to observe without knowing to look for it. We have a key to understanding real-world phenomena. The key is the mathematics."
The researchers plan to refine the models over time as a way of taking initial steps on their way to developing new crime fighting strategies.
Jeff Brantingham, UCLA professor of anthropology and George E. Tita, professor in the department of criminology, law and society at the University of California, Irvine, also participated in the research.
-NSF-
-
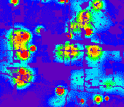
New mathematical models predict formation of crime hotspots and gives clues for police strategies.
Credit and Larger Version
Media Contacts
Bobbie Mixon, NSF, (703) 292-8485, email: bmixon@nsf.gov
Stuart Wolpert, UCLA, (310) 206-0511, email: swolpert@support.ucla.edu
Program Contacts
Rita A. Teutonico, NSF, (703) 292-7118, email: rteutoni@nsf.gov
Principal Investigators
Martin Short, UCLA, (310) 825-9369, email: mbshort@math.ucla.edu
Co-Investigators
Andrea Bertozzi, UCLA, (310) 825-4340, email: bertozzi@math.ucla.edu
The U.S. National Science Foundation propels the nation forward by advancing fundamental research in all fields of science and engineering. NSF supports research and people by providing facilities, instruments and funding to support their ingenuity and sustain the U.S. as a global leader in research and innovation. With a fiscal year 2023 budget of $9.5 billion, NSF funds reach all 50 states through grants to nearly 2,000 colleges, universities and institutions. Each year, NSF receives more than 40,000 competitive proposals and makes about 11,000 new awards. Those awards include support for cooperative research with industry, Arctic and Antarctic research and operations, and U.S. participation in international scientific efforts.
Connect with us online
NSF website: nsf.gov
NSF News: nsf.gov/news
For News Media: nsf.gov/news/newsroom
Statistics: nsf.gov/statistics/
Awards database: nsf.gov/awardsearch/
Follow us on social
Twitter: twitter.com/NSF
Facebook: facebook.com/US.NSF
Instagram: instagram.com/nsfgov